July 8, 2020
Exploring Russia: Tourism ÷ lockdown × accelerator = winners’ podium!
Mid-spring this year, at the very peak of the everyone-at-home period, it became obvious that things were looking very bleak for the world, and would stay bleak for a long time. Business would be hard hit, to put it mildly, while the tourism industry would be fairly devastated, with many a business within it not pulling through the crisis. So we at K did what we often always do – put our thinking caps on – and decided… to help out this most badly affected of industries.
Early May I announced that the ‘Kaspersky Exploring Russia’ tourism accelerator had started accepting applications. But I never guessed that more than 500 would be sent in – from 47 countries (nearly a quarter of all the countries in the world!) on five continents (all bar Antarctica!). And looking through them I realized just how much potential there is in the tourism industry – so many ideas, and so many great startups and existing projects. There were no geographical restrictions for applications: they could have – and did – come from anywhere on the planet, but they had to describe tourism ideas that could either tap the potential of Russian tourism or be applied in Russia. We sifted through all the applications to pick a top-10 very best ideas, and those 10 entered the accelerator program.
And for two weeks the 10 projects took part in online master classes and lectures. Each team had a series of specially tailored consultations with mentors. Leading industry figures shared with participants their experiences and know-how for building up a successful business. Mentors included: Vikas Bhola, regional director of Booking.com; Gemma Rubio, founder of Define the Fine; Vadim Mamontov, general director of Russia Discovery; and other industry professionals. And over those two weeks the participants also polished their presentations, which they then gave to the jury, which I was on.
Last week the finalists gave their presentations and answered our questions in the final demo-day of the accelerator. Out of those, we chose three winners, to which were awarded prizes from our partners. Let me tell you a bit about each of them…
First place was taken by 360 Stories. It’s a mobile augmented reality app with a live guide. They say their mission is to ‘modernize the traditional touring experience by powering interactive live tours using real-time guides’. With 360 Stories folks can now remotely roam their favorite cities and attractions by signing up for a personalized touring experience with a real-time local guide.
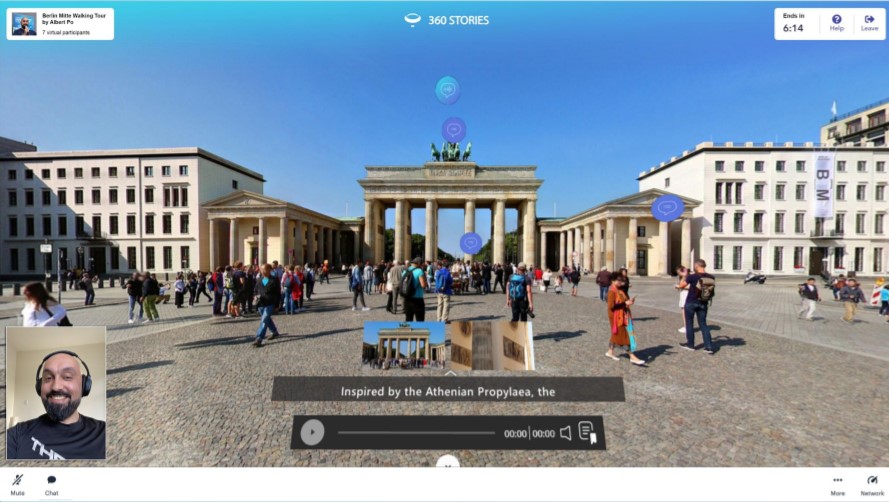
Btw: 360 Stories nearly lost – by oversleeping and not turning up! Its presentation was given at 05:30 local time – New York. Given such an early rise, Mr. 360 Stories slept in, despite having set his alarm. He wakes up eventually, and calls the organizers to ask why he had 20 missed calls on his phone. They were all to tell him he’d won, and ask – ‘where are you?!’



