2017: Leonardo, Fibonacci and Fermat Numbers: It’s Not So Complicated.

In my previous post we had a math competition. Let me remind you of the task:

Using +, -, x, ÷ and (), make the row of numbers from 10 to 1 equal 2017.

That was an easy task, which got more complicated.

How about 9 to 1 with arithmetic equalling 2017? 8 to 1? 7 to 1? And down to just 1?

Before I could say ‘What January blues when you’ve got arithmetic in your life!?!’ I had answers from people in our fan club streaming in! And some of them (remember, there are different possibilities to get the same answer of 2017) were so wonderfully interesting, while others were so interestingly not-quite-elegant enough, that, well, I just had to share some of them with you…

— 10 —

Herewith, the most elegant solutions:

10 * 9 * 8 * 7 * 6 / 5 / (4 – 3 + 2) + 1 = 2017
10 * 9 * 8 * (7 – 6) / 5 * (4 + 3) * 2 + 1 = 2017
(10 – 9) + 8 * 7 * (6 – 5) * 4 * 3 * (2+1) = 2017
(10 – 9) + 8 * 7 * 6 * (5 – 4) * 3 * 2 * 1 = 2017
(-10 + 9 + 8 + 7 * (6 + 5)) * 4 * 3 * 2 + 1 = 2017

Also using all ten numbers, you could do it like this, but it’s most inelegant (er, I came up with this one; only took me ten minutes, mind:) :

((10 + (987) + (6 + 5) * (4 – 3)) * 2) + 1 = 2017

A.B., a colleague who sits just round the corner from my office at HQ, even managed to get in some ‘divided by’ symbols ( /). Ok, so, with those you turn whole numbers into fractions, but, well, why not?

10 * 9 * 8 * 7 / ((6 * 5) / 4) – 3 – 2) + 1 = 2017

And some more elegant math:

10 – (9 + 8 * (7 * (6 * (5 * (4 – (3 + 2)) – 1)))) = 2017
(10 – 9) + 8 * (7 * (6 * ((5 * (4 – 3)) + 2 – 1))) = 2017

— 9 —

Now let’s remove the ’10’. At first it appears that that would make the task more difficult. However, the solution can be reached in just a few minutes, it turns out:

9 * 8 * 7 * 6 * (5 – 4) / 3 * 2 + 1 = 2017
9 + 8 * ((7 * 6 * (5 – 4) * 3 * 2) – 1) = 2017
9 * 8 * 7 * (6 – 5 + 4 – 3) * 2 + 1 = 2017

While A.B. managed a slashy variant too:

9 * 8 * 7 * 6 / (((5 + 4) / 3) / 2) + 1 = 2017

Still on the slashing theme, there’s also this variant:

9 * (8 – ((7 – 6) * (5 – 4))) * (32) + 1 = 2017

— 8 —

With just 1-8, inclusive, things were surprisingly easier than the previous two:

8 * 7 * 6 * (5 – 4) * 3 * 2 +1 = 2017
8 * 7 * (6 + 5 + 4 + 3) * 2 + 1 = 2017
8 * 7 * 6 * ( 5 + 4 – 3) + (2 – 1) = 2017
8 * (7 + 6 + 5) * ((4 * 3) + 2) + 1 = 2017

Wonky arithmetic:

(8 – 7 + 6) * (5 + 4) * (32) + 1 = 2017

— 7 & 6 —

If using just 1-6 or 1-7, a factorial is needed; I couldn’t get to 2017 without it:
7 * (6 – 5) * 4! * 3! * 2 + 1 = 2017
6! / 5 * (4 + 3) * 2 + 1 = 2017

7 – 6 – 5! – 4! + 3 * ((2+1)!)!
7 + (6! – 5 * (4 + 3!)) * (2+1)
7 – (6 – 5!) * 4! – (3!)! – (2+1)!
7! – 6! / 5 – 4 * (3!)! + 2-1
7! – (6 + 5!) * 4! + (3-2-1)!

6! – 5! – 4! + (3!)! * 2 + 1
(6 + 5!) * 4! / 3 * 2 + 1
(6! / 5 + 4!) * 3! * 2 + 1

Any other variants folks?

— 5 —

Just a wonky solution:

/5 * (4 + 3)! * 2 + 1

This one is more elegant but needs a square root:

((( 5 – √4 )! )!!!! ) !!!!! * ((3 * 2)!!!! ) + 1 = 2017.

— 4 —

(How low can you go?!)

[(4#)!!!!]!!!!! * [(3 * 2)!!!!] + 1 = 2017

Where # is a primorial, and !!!! and !!!!! are primorial primes

Bravo! Jolly well done that man! I’d never heard of such types of numbers before! We simply weren’t taught about them; honest!

And a couple of extra solutions:

((4!)!!!!!!!!!!!!!!!!!)*(3!)*2+1 = 2017

It goes like this:

4!=1*2*3*4=24
24!!!!!!!!!!!!!!!!!=24*(24-17)=24*7=168
3!=6
168*6*2+1=2016+1=2017

Extremely elegant solution!

And one more, where sf(n) is a superfactorial:

sf(4) * (3! + !2) + 1 = 2017

where:

sf(4)=1!*2!*3!*4!=288
3!=3*2*1=6
!2=1

— 3 —

But it’s not the end of the story! Now we are about ‘to math’ 2017 from only ‘3, 2 & 1’, no more. Am I serious? Yes!

For this task we’d need:

L(n) – a Leonardo number,
!n – a subfactorial, and
n!! – a primorial prime!

Here we go:

1 + 2 = 3.
L(3) = 5.
5!! = 15.
L(15) = 1973.
!5 = 44.

L( (L(3)) !! ) + !( L(2 + 1) ) = 1973 + 44 = 2017

That was quick and easy. Oh, those men! :)

— 2 —

Two-and-one, how to witchcraft it to 2017? Not possible? Have a look: ‘2 1 = 2017’. Which kind of black math magic do we need to boil this soup?

For this task we need:

A Fibonacci number F(n) and a Fermat number Fm(n)

which leads us to the previous task (3, 2, 1 -> 2017):

F(2) = 1 (otherwise we can use a subfactorial !2=1).
Fm(1) = 3.

2 1 => Fm(F(2)) Fm(1) => 3 3
L( (L(3)) !! ) + !( L(3) ) = ….. guess what? :)

or

L( (L( Fm(F(2)) )) !! ) + !( L( Fm(1) )) = 2017.

And that’s the ‘end of the road’ sign, folks. It’s obvious it is NOT possible to transform a single ‘1’ to ‘2017’, the math space and time isn’t a science fiction movie, and there’s no such teleportation tunnel to jump from ‘1’ to ‘2017’.

Oh, well. There was NO such a tunnel before I shared this idea with colleagues of mine. One of them replied to my story with a trigonometric caterpillar, which is explained in just a few lines below.

Ready? Still don’t believe me? Keep your smiles for better cases – it IS possible! And say ‘wow!’ to Maxim Yurchuk, who made up this crazy math.

— 1 —

ctg arctg sin arcctg ctg arctg sin arcctg … ctg arctg sin arcctg 1 (repeat the function ctg arctg sin arcctg 2017^2 -1 times) = 2017.

And here’s the proof:

sin t = 1/sqrt(1+ ctg^2(t)),
translate the two functions on the right and we get:
sin arcctg s = 1/sqrt(1 + s^2)

Using ctg arctg (s) = 1/s, we get:
ctg arctg sin arcctg s = sqrt(1 + s^2)

Using the same logic, we can be sure that these four functions, twice, leads us to
ctg arctg sin arcctg ctg arctg sin arcctg s = sqrt(2 + s^2)

Using mathematical induction, we can prove:
ctg arctg sin arcctg .. ctg arctg sin arcctg s = sqrt(n + s^2)
where ctg arctg sin arcctg repeat n times.

Then we replace s with 1 and get:
ctg arctg sin arcctg .. ctg arctg sin arcctg s = sqrt(n + 1^2)
where ctg arctg sin arcctg repeat n times.

Repeat these four functions 2017^2-1 times (i.e., n = 2017^2-1), and this leads us to
sqrt(2017^2-1 + 1^2) = sqrt(2017^2) = 2017.

Bingo!

More proof, (more ‘illustrative’):

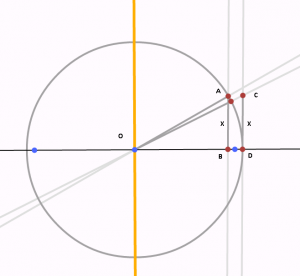
Let’s show that ctg arctg sin arcctg Vn = V(n+1).

The picture below clarifies the problem: the cotangent of the AOB angle equals Vn, i.e., OB / AB = V(1-x^2) / x = Vn. Ergo, we need to calculate the cotangent of the COD angle considering that AB = CD = x. This cotangent equals OD/CD = 1/x. This leads us to 1/x = V(n+1) because (1 – x^2) / x^2 = n.

— 0 —

The ‘cherry on a cake’, zero to twenty-seventeen. This one’s easy:

cos(0)=1

Then we go back to the previous task.

— Bonus Track —

Let’s continue this theme somehow.

How about… getting 2017 from i (don’t forget to click on the link as this is a very interesting i)? How do we turn 2017 into the Planck constant? Or the mass of an electron in atomic units? Or the % of VAT concessions on export operations – in short, the ocean of mathematical illusions in the modern physics-social-economic-sphere is absolutely limitless. Come on, try!

We still have time till the end of this year, when we’ll need to redo the arithmetic for 2018 :).